|
The magic square is represented by n x n matrix. The normal magic square contains
numbers from 1 to n2 (Ellis et al., 2002). There exists a magic square for all orders
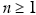 , except n = 2. Several methods exist for construction of magic square of any
given order (www.wikipedia.org). , except n = 2. Several methods exist for construction of magic square of any
given order (www.wikipedia.org).
The magic squares have several applications in fields of discrete and combinatorial
mathematics, and also in the area of graph theory. One such application of magic
square is in graph labeling. It has been proved using the magic square of order n
that, “There exists a vertex magic total labeling for all complete graph Kn”
(Krishnappa et al., 2009 and 2010).
Our process of constructing a magic square of order n is divided into the following
categories and subcategories:
Magic square of order n, where n is odd.
Magic square of order N, where N is even.
Magic square of order 4.
Magic square of order N, for all 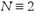 mod 4. mod 4.
Magic square of order N, for all 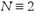 mod 4. mod 4. |





