This paper aims at developing a framework for evaluating derivatives if the underlying clause of the derivative contract is supposedly driven by a fractional Brownian motion (fBm) with Hurst parameter greater than 0.5. For this purpose, some results regarding the quasi-conditional expectation, especially the behavior to a Girsanov transform, are proved. The risk-neutral valuation formula and the fundamental evaluation equation in the case of the fractional Black-Scholes (BS) market, are then obtained.

The self-similarity and long-range dependence properties make the fBm a suitable tool in different applications like mathematical finance. Since for 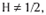the fBm is neither a Markov process, nor a semimartingale (see for example, Rogers, 1997), we cannot use the usual stochastic calculus to analyze it. Worse still, after a path-wise integration theory for fBm was developed by Lin (1995) and Decreusefond and Ustunel (1999), it was proved by Rogers (1997) that the market mathematical models driven by B_H(t) could have arbitrage. The fBm was no longer considered suitable for mathematical modeling in finance. However, after the development of a new kind of integral based on the Wick product called the fractional Ito integral, by Duncan et al. (2000) and Hu and Oksendal (2003), it was proved in Hu and Oksendal (2003) that the corresponding Ito type fractional Black-Scholes (BS) market has no arbitrage. Equivalent definitions of the fractional Ito integral were introduced by Alos et al. (2000), Perez-Abreau and Tudor (2002), and Bender (2002). Hu and Oksendal (2003) introduced the concept of quasi-conditional expectation and quasi-martingales. In the same paper, a formula for the price of a European option at t = 0 has been derived.

In Section 2 of this paper, we prove some results regarding the quasi-conditional expectation, especially the behavior to a Girsanov transform. In Section 3, we apply these results to obtain the risk-neutral valuation formula and the fundamental evaluation equation in the case of the fractional BS market. The final section comprises conclusions drawn from the study.

A Framework for Derivative Pricing in the Fractional Black-Scholes Market, quasi-conditional expectation, fractional Brownian motion (fBm), Hurst parameter, Hu and Oksendal, fractional BS market, Girsanov transform, risk-neutral valuation, semimartingale.